JS逆向

JS逆向：JS 逆向方式破解某验滑块验证码

1. 抓包分析

打开某验的 demo，点出验证码图片，分析 network 中的请求以及参数变化 请求与参数：

1、	Request URL: https://www.geetest.com/demo/gt/register-slide?t=1640096834809
	返回：	challenge: "5bd76b0b1c9388a667bba39af5cfd71e"
			gt: "019924a82c70bb123aae90d483087f94"
			
2、	Request URL: https://apiv6.geetest.com/gettype.php?gt=019924a82c70bb123aae90d483087f94&callback=geetest_1640096837076
	返回：	fullpage: "/static/js/fullpage.9.0.8.js"
			slide: "/static/js/slide.7.8.6.js"
			
3、	Request URL: https://apiv6.geetest.com/get.php?gt=019924a82c70bb123aae90d483087f94&challenge=5bd76b0b1c9388a667bba39af5cfd71e&lang=zh-cn&pt=0&client_type=web&w=7(Pr5uTDzYQIrCym5Psn(W7fvv7K3ji2dFDhp...
	提交：	gt: 019924a82c70bb123aae90d483087f94
			challenge: 5bd76b0b1c9388a667bba39af5cfd71e
			w: 7(Pr5uTDzYQIrCym5Psn(W7fvv7K3ji2dFDhpCxfIsWhd...
	返回：	status: "success"
	
4、	Request URL: https://api.geetest.com/ajax.php?gt=019924a82c70bb123aae90d483087f94&challenge=5bd76b0b1c9388a667bba39af5cfd71e&lang=zh-cn&pt=0&client_type=web&w=7ZMNp(76n(MlO6aTxrUCxNw(7Jj5kEFnmodPZj2Nid...
	提交：	w: 7ZMNp(76n(MlO6aTxrUCxNw(7Jj5kEFnmodPZj2NidffUg3PXYPHS(65Up0jO2X...
			callback: geetest_1640096847867

5、	Request URL: https://api.geetest.com/get.php?is_next=true&type=slide3&gt=019924a82c70bb123aae90d483087f94&challenge=5bd76b0b1c9388a667bba39af5cfd71e&lang=zh-cn&https=true&protocol=https%3A%2F%2F&offline=false&product=embed&api_server=api.geetest.com&isPC=true&autoReset=true&width=100%25&callback=geetest_1640096847383
	提交：	gt: 019924a82c70bb123aae90d483087f94
			challenge: 5bd76b0b1c9388a667bba39af5cfd71e
	返回：	fullbg: "pictures/gt/b9694f3e8/b9694f3e8.jpg"
			slice: "pictures/gt/b9694f3e8/slice/f35f84584.png"
			bg: "pictures/gt/b9694f3e8/bg/f35f84584.jpg"

拖动滑块，完成验证，继续分析请求和参数。

6、	Request URL: https://api.geetest.com/ajax.php?gt=019924a82c70bb123aae90d483087f94&challenge=5bd76b0b1c9388a667bba39af5cfd71eaj&lang=zh-cn&%24_BBF=0&client_type=web&w=(x5U5)0n0zt1KeeU1X7ZseyXl)fhHOh539)Bm2(6...
	提交：	w: (x5U5)0n0zt1KeeU1X7ZseyXl)fhHOh539)Bm2(6bQrrmShGp9v27nhkmGV...
			gt: 019924a82c70bb123aae90d483087f94
			challenge: 5bd76b0b1c9388a667bba39af5cfd71eaj
			
	返回：	message: "success"
			validate: "00c14c420b44ade8cd6d3ddd5c916010"

需要明确的问题： 1、还原底图（处理底图乱序问题）； 2、获取 w 值，生成轨迹；

2. 还原底图

  • 通过分析页面元素，我们发现验证码是一个 canvas。

  • 我们打上 canvas 断点，然后刷新重新获取验证码。

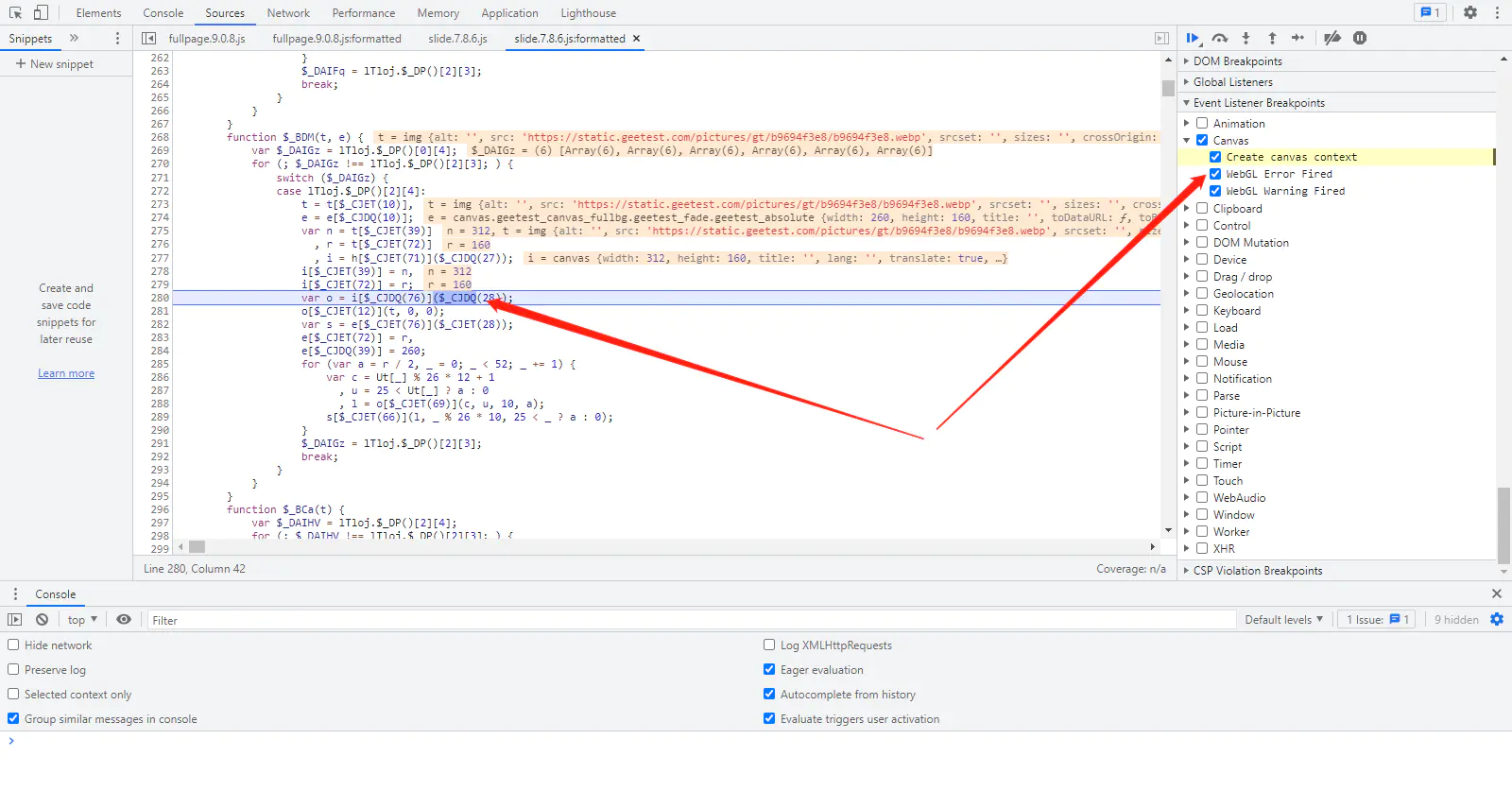
  • 此时注意提示 https://static.geetest.com/pictures/gt/b9694f3e8/b9694f3e8.webp 打开以后就是乱序验证码， e = canvas.geetest_canvas_bg.geetest_absolute {width: 260, height: 160, title: '', toDataURL: ƒ, toBlob: ƒ, …} 的就是验证码的宽度和高度。 同时，仔细观察我们发现，验证码混淆后分成了上下两部分。

  • 单步调试，集合验证码图片、分析代码；

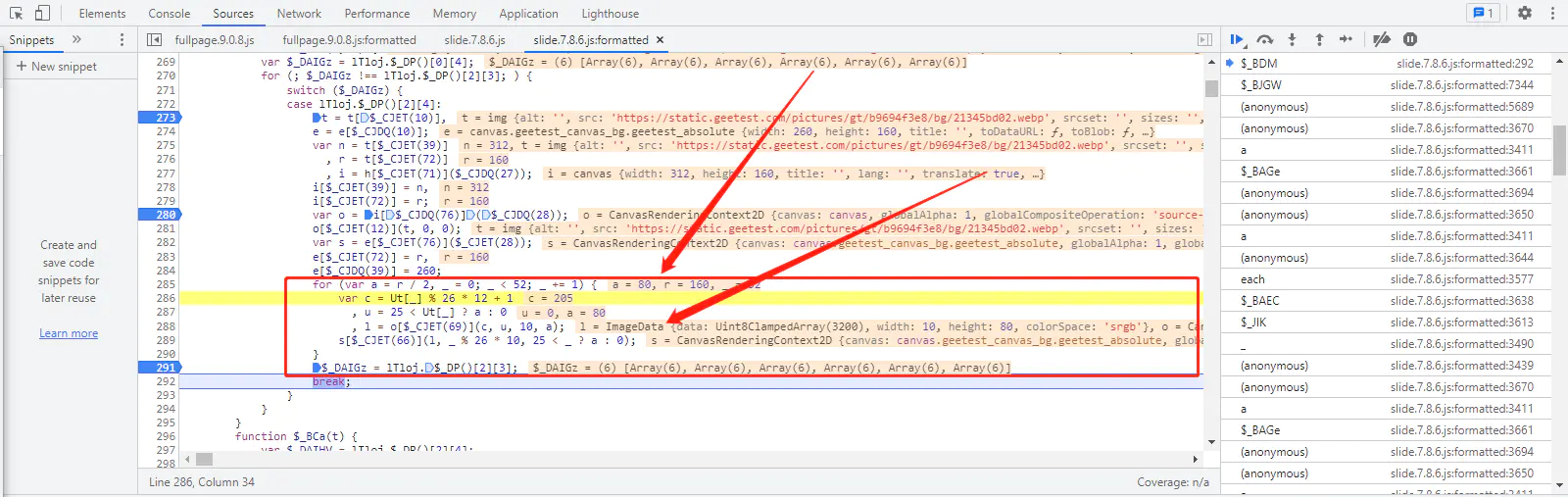
根据提示我们发现，有一段代码的提示是 l = ImageData {data: Uint8ClampedArray(3200), width: 10, height: 80, colorSpace: 'srgb'}, o = CanvasRenderingContext2D {canvas: canvas, globalAlpha: 1，推测 ImageData 是画图动作，进而推测验证码还原的关键步骤，在 l = o[$_CJET(69)](c, u, 10, a) 这一步。 我们仔细分析一下这一段 for 循环代码。

                    for (var a = r / 2, _ = 0; _ < 52; _ += 1) {
                        var c = Ut[_] % 26 * 12 + 1
                          , u = 25 < Ut[_] ? a : 0
                          , l = o[$_CJET(69)](c, u, 10, a);
                        s[$_CJET(66)](l, _ % 26 * 10, 25 < _ ? a : 0);
                    }

对上面的代码进一步分析，我们发现这里进行了 52 次循环，而代码中的 26 刚好是 52 的一半，这个与前面验证码被分成上下两部分呼应。 我们推测验证码被分成了52个小块，上下两个部分各有26，每个小块是的宽度是 10，加在一起正好是 260，刚好是前面分析发现的整个验证码图片的宽度。

仔细分析上面的代码，我们发现这个循环，会根据 Ut[_] 的变化而进行不同的操作。_ 是一个每次自增1且小于52的整数，那 Ut 是什么呢？ 我们在 console 中获取，发现他是一个52位的数组， [39, 38, 48, 49, 41, 40, 46, 47, 35, 34, 50, 51, 33, 32, 28, 29, 27, 26, 36, 37, 31, 30, 44, 45, 43, 42, 12, 13, 23, 22, 14, 15, 21, 20, 8, 9, 25, 24, 6, 7, 3, 2, 0, 1, 11, 10, 4, 5, 19, 18, 16, 17]。 这个时候，就可以断定这个数组就是验证码混淆的顺序，按照这个顺序反向操作就能还原验证码。而上面的 for 循环，实际就是在执行这个还原验证码的操作。

注意： 这个数组可能是动态的，也可能是静态的，为了验证是静态还是动态，我们需要进行多次调试，对比该数组是否发生变化。这里我们通过分析，确认该数组是静态的。

至此，底图还原的逆向工作完成。

3. 获取 w 值 & 还原推动轨迹

3.1. 获取 w 值

w 值在这里曾经多次生成，这里只分析其中的一次。 w 是一个数字单字符，这里通过直接搜索无法直接搜到。这里我们采用跟栈的方式一步步回溯。

跟栈技巧

跟栈的时候，注意我们的重点关注 w 值有没有在提示中出现，如果又出现就说明它在代码之前或者上一步，就已经被生成了。我们就继续往前找，一直找到提示中没有 w 值的时候，我们再分析 w 值到底是在哪里生成的。

注意：在开始跟栈的时候，如果找不到 w 值，就往前多跟几步。

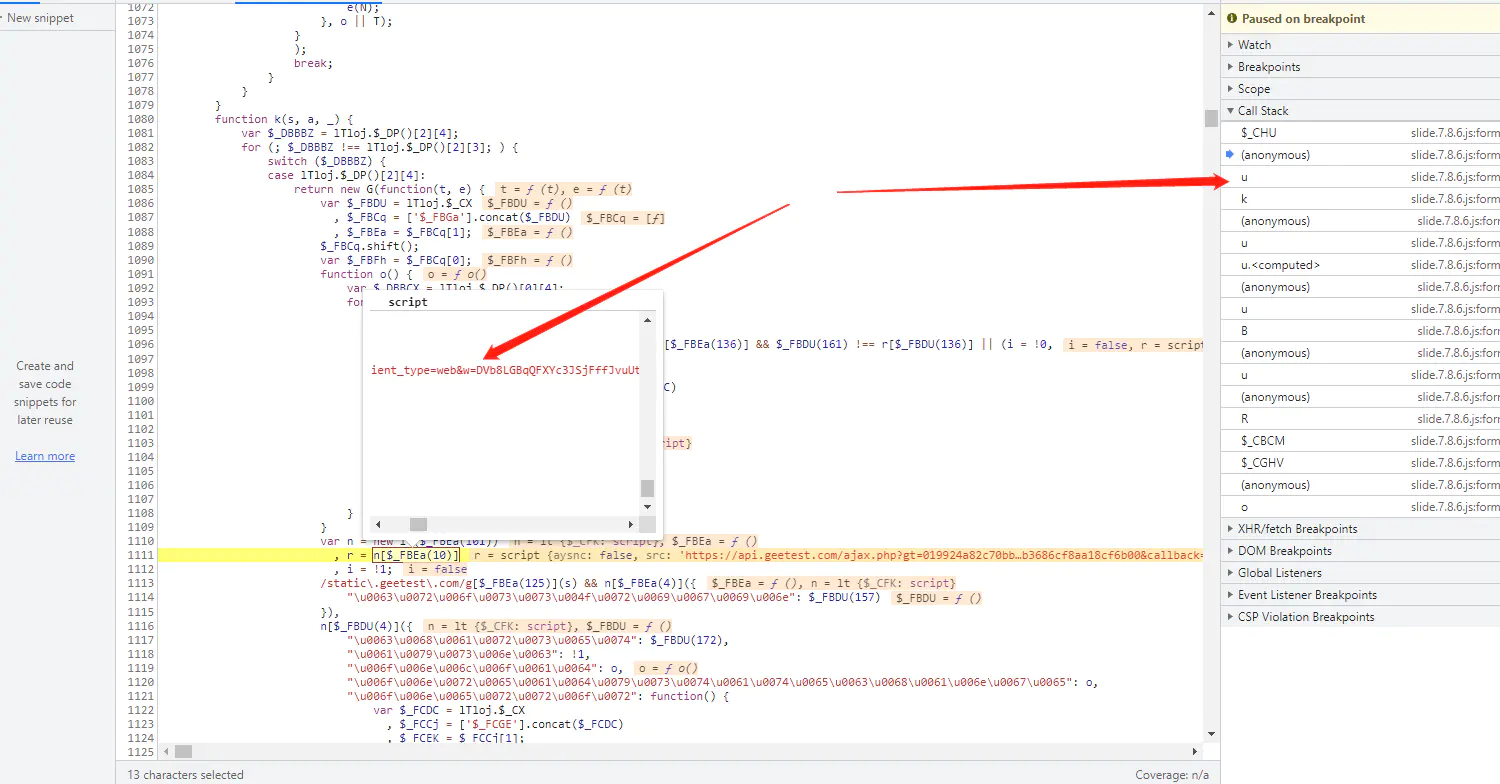
继续上面的思路往前跟栈，很快就会发现遇到一个平坦流，如下图：

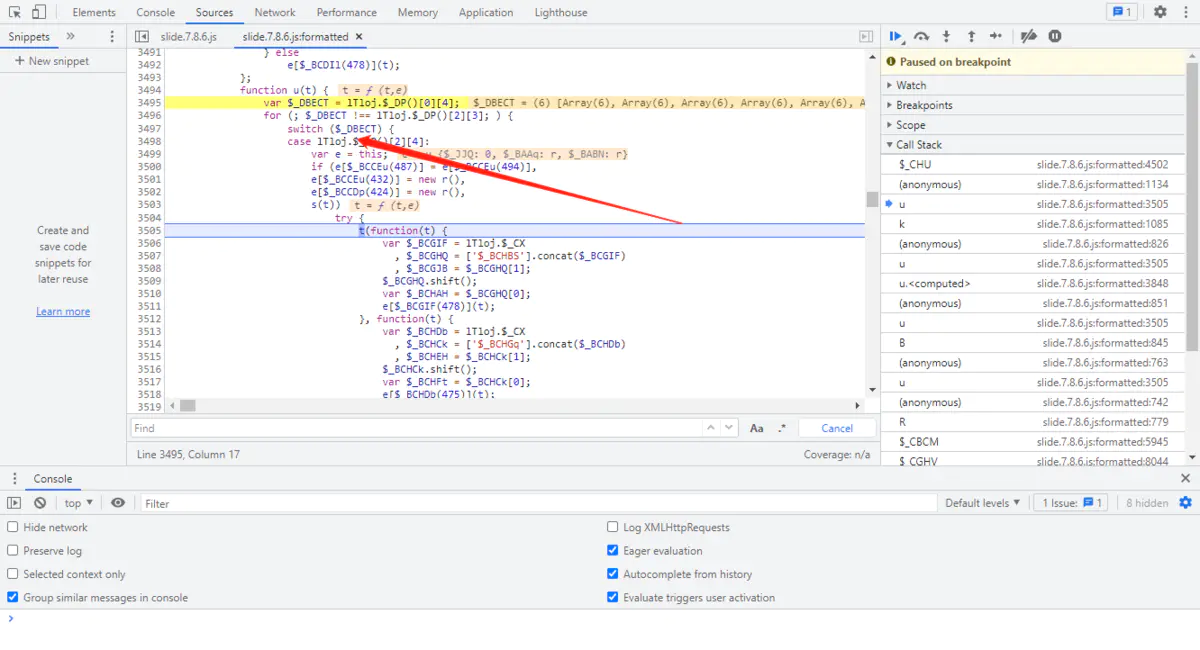
平坦流的跟栈技巧

当遇到平坦流的时候，首先调试分析平坦流有没有对目标参数做修改，如果没有就不用关注控制流，直接跳过就好。 很多时候，我们可以直接跳过平坦流，继续往前找，看看能不能找到 w 值，如果实在找不到再回来分析平坦流。这里其实可以先在函数内部、平坦流前打一个断点，然后刷新货重新请求、让浏览器在此处被断掉，继而进行跟栈分析。 分析发现，w 值在 R 这层已经出现，那我们就没必要关注之前的平坦流，接着跟栈分析就可以。如下图：

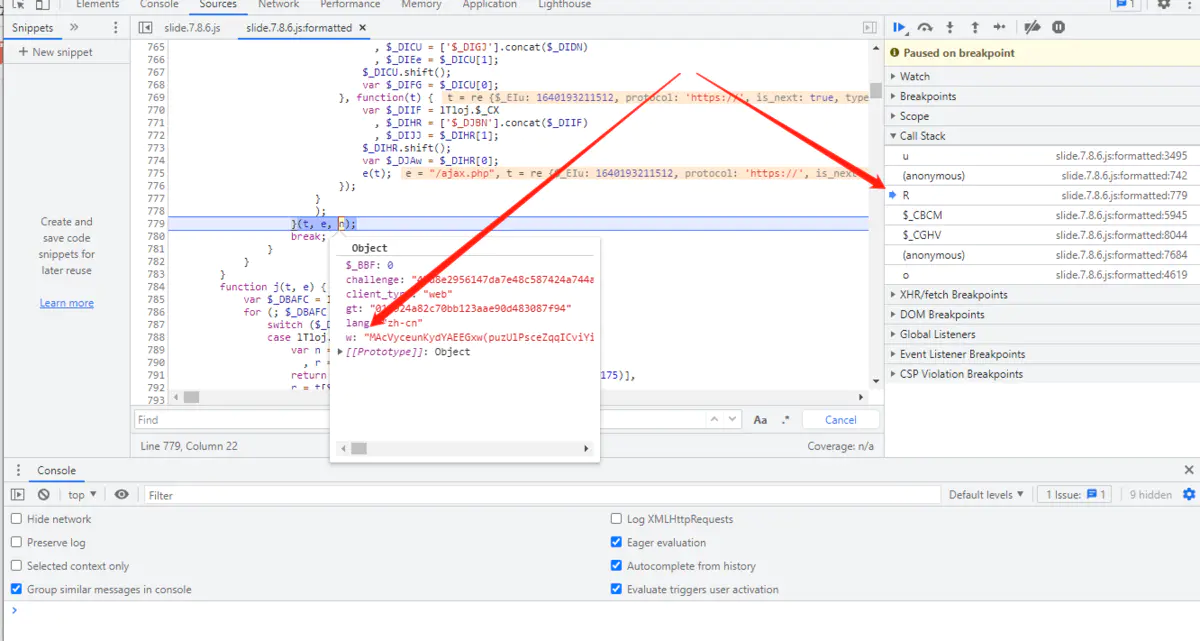
我们接着进行跟栈分析，发现调试工具已经把 "w" 的生成逻辑都提示出来了。

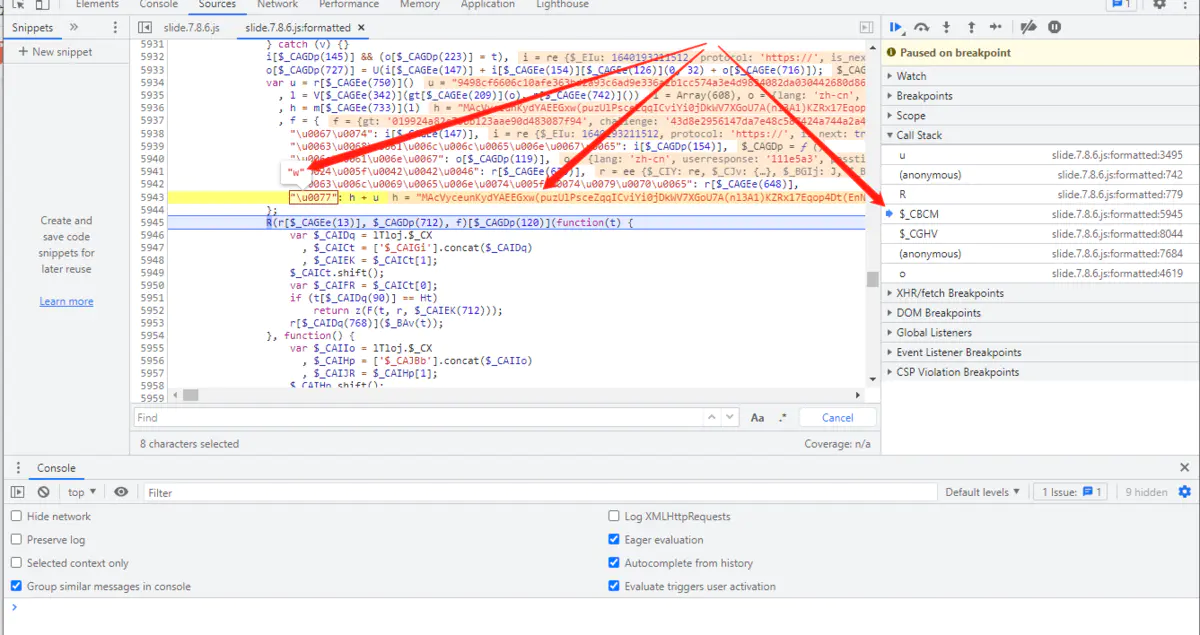
w 值的生成代码就是下面这行。

 "\u0077": h + u

到这一步，就进入你想的关键步骤了。 下面附上比较关键的一段加密代码，供大家参考。

        var rt = function() {
            var $_BFBDL = lTloj.$_CX
              , $_BFBCi = ['$_BFBGO'].concat($_BFBDL)
              , $_BFBEt = $_BFBCi[1];
            $_BFBCi.shift();
            var $_BFBFk = $_BFBCi[0];
            function t() {
                var $_DBFAh = lTloj.$_DP()[0][4];
                for (; $_DBFAh !== lTloj.$_DP()[2][3]; ) {
                    switch ($_DBFAh) {
                    case lTloj.$_DP()[0][4]:
                        return (65536 * (1 + Math[$_BFBDL(75)]()) | 0)[$_BFBDL(396)](16)[$_BFBDL(476)](1);
                        break;
                    }
                }
            }
            return function() {
                var $_BFBIl = lTloj.$_CX
                  , $_BFBHs = ['$_BFCBY'].concat($_BFBIl)
                  , $_BFBJq = $_BFBHs[1];
                $_BFBHs.shift();
                var $_BFCAQ = $_BFBHs[0];
                return t() + t() + t() + t();
            }
            ;
        }();

3.2. 轨迹还原

当分析到前面代码处位置时，我们发现其中一个很重要的参数 o，这个 o 是一个对象，对象中其中包括了下面的内容。

aa: "M/-821./0(!!Mty!)(!)!)!)!K)(!)ysttststsss(!!(f011/11x1111/19111o6,S/$)ZC"
ep: {v: '7.8.6', $_BHR: false, me: true, tm: {…}, td: -1}
imgload: 813
lang: "zh-cn"
passtime: 337
rp: "a110d6f451e2b042883f4ae191a89272"
userresponse: "99e999e71"
xb3y: "1140037174"
[[Prototype]]: Object

通过多次调试，我们发现这里的 aa 和 rp 值，会随着每次拖动滑块验证码而变化，我们猜测这里可能是滑动的轨迹。通过想上查找和跟栈，我们找到了这个地方：

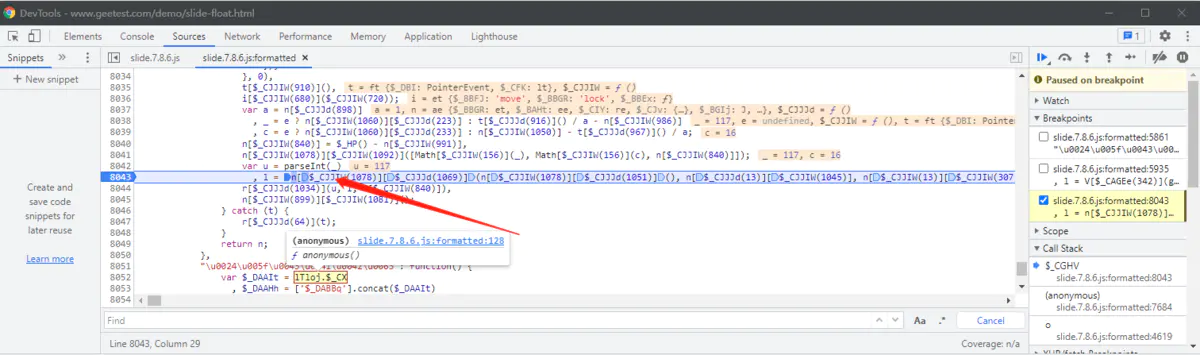
l = n[$_CJJIW(1078)][$_CJJJd(1069)](n[$_CJJIW(1078)][$_CJJJd(1051)](), n[$_CJJJd(13)][$_CJJIW(1045)], n[$_CJJIW(13)][$_CJJIW(307)])

通过还原，得到以下代码：

l = n['$_CIBw']['$_BBCA'](n['$_CIBw']['$_GEy'](), n['$_CIY']['c'], n['$_CIY']['s'])

通过 console 控制台，我们分析得到下面的内容：

n['$_CIBw']['$_GEy']() :   'T,0./53/220-,(!!Mty*)))*)))(y((t)tssssswssssswsssssvvsssswsss(!!($)39/112011100120112.9191/:8Fp/01Ei:-:901C3/_$)J$*r'
n['$_CIY']['c']        :   [12, 58, 98, 36, 43, 95, 62, 15, 12]
n['$_CIY']['s']        :   '6f404c79'

那上面的数据都是从哪里拿到的呢？我们将 n['$_CIY'] 还原，得到下面的内容：

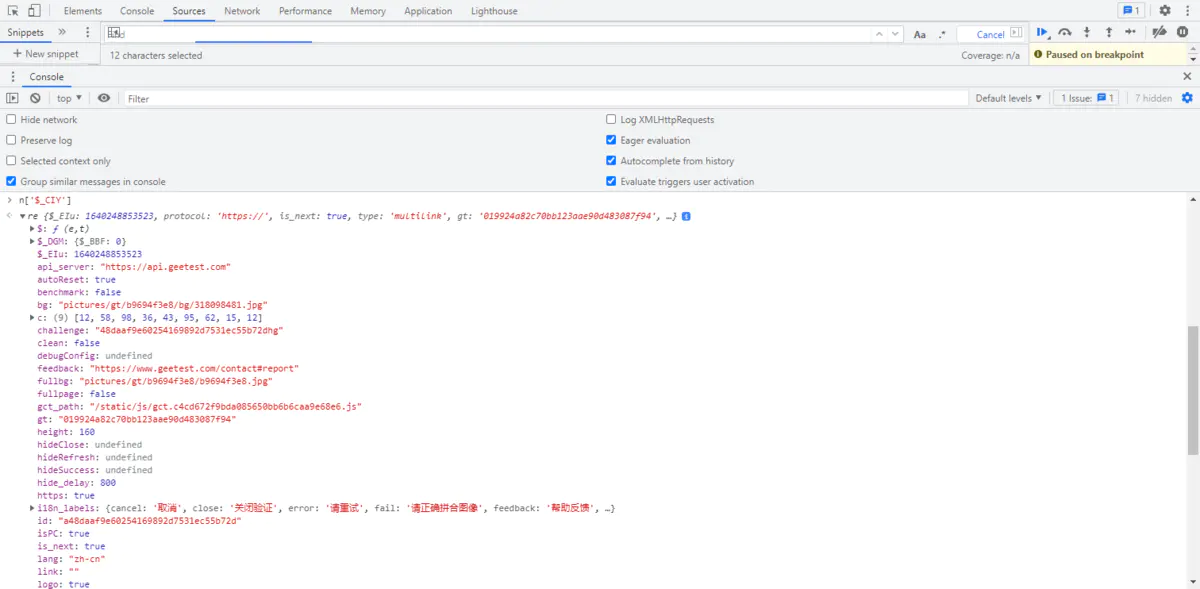
通过分析，可以知道 n['$_CIY']['c']、n['$_CIY']['s'] 是前面通过请求返回的，可以直接拿来使用。 这里比较重要的是 n['$_CIBw']['$_GEy']() ，我们进入函数找到下面这段代码。

"\u0024\u005f\u0047\u0045\u0079": function() {
                var $_BEGIH = lTloj.$_CX
                  , $_BEGHL = ['$_BEHBT'].concat($_BEGIH)
                  , $_BEGJJ = $_BEGHL[1];
                $_BEGHL.shift();
                var $_BEHAr = $_BEGHL[0];
                function n(t) {
                    var $_DBEIz = lTloj.$_DP()[0][4];
                    for (; $_DBEIz !== lTloj.$_DP()[2][3]; ) {
                        switch ($_DBEIz) {
                        case lTloj.$_DP()[0][4]:
                            var e = $_BEGJJ(430)
                              , n = e[$_BEGJJ(182)]
                              , r = $_BEGIH(33)
                              , i = Math[$_BEGIH(383)](t)
                              , o = parseInt(i / n);
                            n <= o && (o = n - 1),
                            o && (r = e[$_BEGIH(122)](o));
                            var s = $_BEGIH(33);
                            return t < 0 && (s += $_BEGJJ(456)),
                            r && (s += $_BEGJJ(459)),
                            s + r + e[$_BEGIH(122)](i %= n);
                            break;
                        }
                    }
                }
                var t = function(t) {
                    var $_BEHDi = lTloj.$_CX
                      , $_BEHCK = ['$_BEHGM'].concat($_BEHDi)
                      , $_BEHEF = $_BEHCK[1];
                    $_BEHCK.shift();
                    var $_BEHFx = $_BEHCK[0];
                    for (var e, n, r, i = [], o = 0, s = 0, a = t[$_BEHEF(182)] - 1; s < a; s++)
                        e = Math[$_BEHEF(156)](t[s + 1][0] - t[s][0]),
                        n = Math[$_BEHDi(156)](t[s + 1][1] - t[s][1]),
                        r = Math[$_BEHDi(156)](t[s + 1][2] - t[s][2]),
                        0 == e && 0 == n && 0 == r || (0 == e && 0 == n ? o += r : (i[$_BEHEF(140)]([e, n, r + o]),
                        o = 0));
                    return 0 !== o && i[$_BEHDi(140)]([e, n, o]),
                    i;
                }(this[$_BEGJJ(361)])
                  , r = []
                  , i = []
                  , o = [];
                return new ct(t)[$_BEGIH(84)](function(t) {
                    var $_BEHIs = lTloj.$_CX
                      , $_BEHHw = ['$_BEIBE'].concat($_BEHIs)
                      , $_BEHJy = $_BEHHw[1];
                    $_BEHHw.shift();
                    var $_BEIAO = $_BEHHw[0];
                    var e = function(t) {
                        var $_BEIDv = lTloj.$_CX
                          , $_BEICk = ['$_BEIGW'].concat($_BEIDv)
                          , $_BEIEU = $_BEICk[1];
                        $_BEICk.shift();
                        var $_BEIFh = $_BEICk[0];
                        for (var e = [[1, 0], [2, 0], [1, -1], [1, 1], [0, 1], [0, -1], [3, 0], [2, -1], [2, 1]], n = 0, r = e[$_BEIDv(182)]; n < r; n++)
                            if (t[0] == e[n][0] && t[1] == e[n][1])
                                return $_BEIEU(413)[n];
                        return 0;
                    }(t);
                    e ? i[$_BEHIs(140)](e) : (r[$_BEHJy(140)](n(t[0])),
                    i[$_BEHJy(140)](n(t[1]))),
                    o[$_BEHJy(140)](n(t[2]));
                }),
                r[$_BEGJJ(444)]($_BEGIH(33)) + $_BEGIH(407) + i[$_BEGIH(444)]($_BEGJJ(33)) + $_BEGIH(407) + o[$_BEGIH(444)]($_BEGIH(33));
            }

其中最后一行代码，经过 console 还原，可以还原呈现面的代码：

r['join']('') + '!!' + i['join']('') + '!!' + o['join']('')

这里的 r、i、o 是三个数组，加密的核心逻辑，就是生成这三个数组。而这三个数组的生成过程，其实也就是对滑动轨迹的处理过程。那轨迹是什么呢？ 通过分析 return new ct(t)[$_BEGIH(84)] 我们发现，整个处理过程都是围绕 t 展开的。

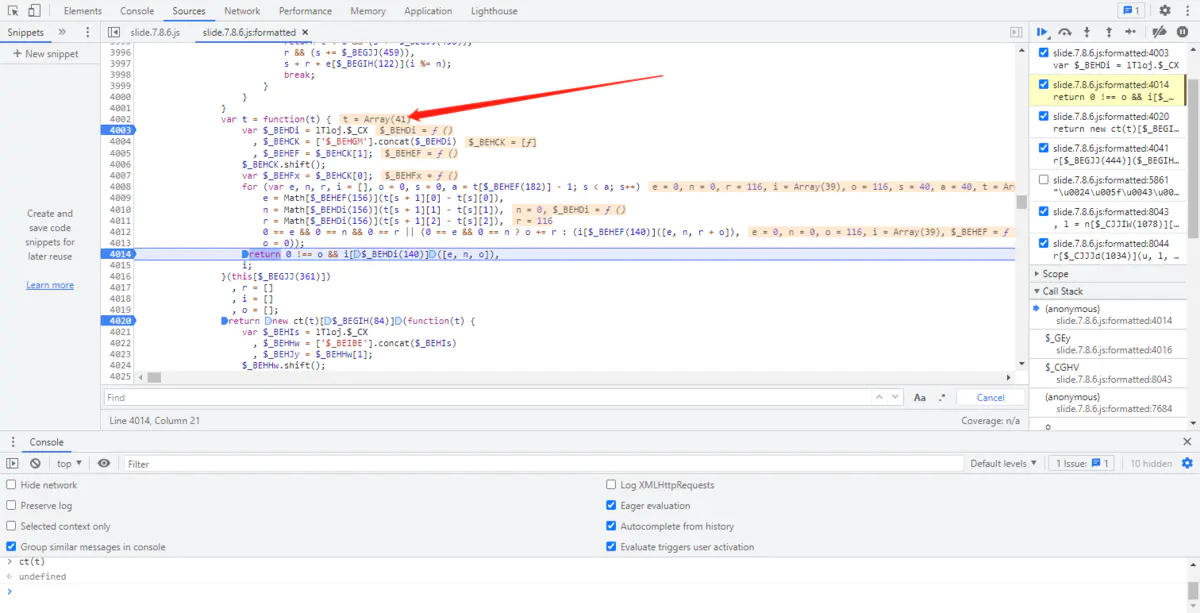
那 t 又是什么东西呢？调试工具已经提示给我们了，它是一个数组，分析数组内容我们推测，这就是滑块运行轨迹，数组中的每个小数组有三个值。 经验判断三个值分别是：横向滑动距离、纵向滑动距离、以及滑动时间。

0: (3) [35, 23, 0]
1: (3) [1, 0, 83]
2: (3) [1, 0, 8]
3: (3) [2, 1, 8]
4: (3) [2, 0, 8]
5: (3) [2, 0, 6]
6: (3) [2, 0, 8]
7: (3) [2, 0, 8]
8: (3) [2, 0, 8]
9: (3) [0, 1, 8]
10: (3) [1, 0, 8]
11: (3) [1, 1, 22]
12: (3) [1, 0, 8]
13: (3) [1, 0, 16]
14: (3) [0, 1, 8]
15: (3) [1, 0, 8]
16: (3) [2, 0, 8]
17: (3) [1, 0, 6]
18: (3) [1, 0, 8]
19: (3) [2, 0, 10]
20: (3) [1, 0, 6]
21: (3) [1, 0, 24]
22: (3) [1, 0, 8]
23: (3) [1, 0, 14]
24: (3) [1, 0, 17]
25: (3) [1, 0, 23]
26: (3) [1, 0, 11]
27: (3) [1, 0, 19]
28: (3) [1, 0, 16]
29: (3) [1, 0, 8]
30: (3) [1, 0, 7]
31: (3) [1, 0, 8]
32: (3) [2, 0, 8]
33: (3) [2, 0, 15]
34: (3) [1, 0, 24]
35: (3) [1, 0, 22]
36: (3) [1, 0, 16]
37: (3) [1, 0, 8]
38: (3) [1, 0, 8]
39: (3) [0, 0, 116]
length: 40
[[Prototype]]: Array(0)

这里需要注意的是，t 的值在经过 ct(t)[$_BEGIH(84)] 函数处理时，会发生变化，如果忽略了这一点可能会导致轨迹加密后，依然无法成功请求。 到这里关键的逆向工作就差不多完成了，不过这里要注意加密的入口是 l = n[$_CJJIW(1078)][$_CJJJd(1069)](n[$_CJJIW(1078)][$_CJJJd(1051)](), n[$_CJJJd(13)][$_CJJIW(1045)], n[$_CJJIW(13)][$_CJJIW(307)])，我们前面的逆向完成的是传入的三个参数，外面的函数也需抠出来。我们下断追进去，发现下面这段代码，直接拿过来用就可以。

"\u0024\u005f\u0042\u0042\u0043\u0041": function(t, e, n) {
                var $_BEIIp = lTloj.$_CX
                  , $_BEIHl = ['$_BEJBo'].concat($_BEIIp)
                  , $_BEIJO = $_BEIHl[1];
                $_BEIHl.shift();
                var $_BEJAQ = $_BEIHl[0];
                if (!e || !n)
                    return t;
                var r, i = 0, o = t, s = e[0], a = e[2], _ = e[4];
                while (r = n[$_BEIIp(373)](i, 2)) {
                    i += 2;
                    var c = parseInt(r, 16)
                      , u = String[$_BEIIp(206)](c)
                      , l = (s * c * c + a * c + _) % t[$_BEIIp(182)];
                    o = o[$_BEIIp(373)](0, l) + u + o[$_BEIJO(373)](l);
                }
                return o;
            }
CATALOG
    FEATURED TAGS
    推荐系统 数据结构 用户画像 指标体系 数仓建模 用户运营 SQL 数据埋点 HBase Hive OLAP 数仓运维 BI FineBI Hadoop Spark Tableau 数仓 数据中台 数据治理 数据湖 数据集市 Airflow DataX DolphinScheduler Flume Kafka Maxwell Zookeeper 任务调度 Elasticsearch ETL 数据产品 数据库 MySQL Python Redis JS逆向 安卓逆向 爬虫 HTTP
    FRIENDS