1. 布隆过滤产生的背景

布隆过滤在位图的基础上产生
- 对于数字的话，位图是可以处理的，因为他们是不存在冲突的，每一个数字对于一个唯一的哈希地址；
- 但是对于字符串，位图是没有办法处理的，因为字符串存在哈希冲突。
- 因此，我们只能通过我们将一个元素经过多个散列函数映射到多个位上来降低误判的概率，布隆过滤器正是基于这个特点应用而生的。
布隆过滤器的基本思想是：
- 通过一个 Hash 函数将一个元素映射成一个位图矩阵中的一个点；
- 我们只需查看这个位置是 1 还是 0 就知道集合中是否存在它，到这里读者朋友应该已经明白了布隆过滤和位图算法之间的关系；
但是由于哈希冲突的原因，即不同的元素经过散列函数后可能产生相同的哈希地址，我们很可能导致误判；
为了降低误判的概率，我们将一个元素经过多个散列函数映射到多个位上，
- 如果这几个位都为1，我们认为它是存在的；
- 如果有一位为0，我们认为它不存在。

2. 布隆过滤的工作原理

布隆过滤器（Bloom Filter）是由布隆（Burton Howard Bloom）在1970年提出，由一个很长的二进制向量（位向量）和一系列随机映射函数组成，可以用于检索一个元素是否在一个集合中；
其工作过程，是将一个元素用多个哈希函数映射到一个位图中,分别计算每个哈希值对应的比特位置存储的是否为零，只要有一个为零，代表该元素一定不在哈希表中，否则可能在哈希表中；

哈希表 的缺点是浪费空间；

位图的缺点是 不能处理哈希冲突；

将 哈希与位图结合，即是此处要讲的布隆过滤器；

布隆过滤器的基本思想，是在位图中添加多个哈希函数，减小需要开辟的存储空间。

具体步骤：
- 我们使用 K 个哈希函数，对同一个输入元素进行求哈希值，那会得到 K 个不同的哈希值，我们分别记作 Y1，Y2，Y3，…，YK；
- 我们把这 K 个数字作为位图中的下标，将对应的 BitMap[Y1]，BitMap[Y2]，BitMap[Y3]，…，BitMap[YK]都设置成 true，也就是说，我们用 K 个二进制位，来表示一个数字的存在；
- 当我们要查询某个数字是否存在的时候，我们用同样的 K 个哈希函数，对这个数字求哈希值，分别得到 Z1，Z2，Z3，…，ZK；
- 我们看这 K 个哈希值，对应位图中的数值是否都为 true，如果都是 true，则说明这个数字存在，如果有其中任意一个不为 true，那就说明这个数字不存在。
误判问题：
- 在上面的步骤中有个问题，如果某个数字经过布隆过滤器判断不存在，那说明这个数字真的不存在，不会发生误判；
- 如果某个数字经过布隆过滤器判断存在，这个时候才会有可能误判，有可能并不存在；
- 不过，只要我们调整哈希函数的个数、位图大小跟要存储数字的个数之间的比例，那就可以将这种误判的概率降到非常低。

优点是空间效率和查询时间都远远超过一般的算法；
- 布隆过滤器存储空间和插入/查询时间都是常数，增加和查询元素的时间复杂度为:O(K), (K为哈希函数的个数，一般比较小)，与数据量大小无关；
- 布隆过滤器的特点是高效地插入和查询，可以用来告诉你 “某样东西一定不存在或者可能存在”，它是用多个哈希函数，将一个数据映射到位图结构中，此种方式不仅可以提升查询效率，也可以节省大量的内存空间；
另外, Hash 函数相互之间没有关系，方便由硬件并行实现；
布隆过滤器不需要存储元素本身，在某些对保密要求非常严格的场合有优势；
数据量很大时，布隆过滤器可以表示全集，其他数据结构不能；
使用同一组散列函数的布隆过滤器可以进行交、并、差运算；

所谓误判，就是要查找的元素并不存在，但是以前插入的数据刚好将 key 经过几个映射函数的 bit 位置为 1，这就造成一种假象，要查找的数据存在；
当输入的数据量比较小的时候，这种情况发生的概率还是比较低的，但是当输入的数据量很大的时候，这种错误率就明显上升了；
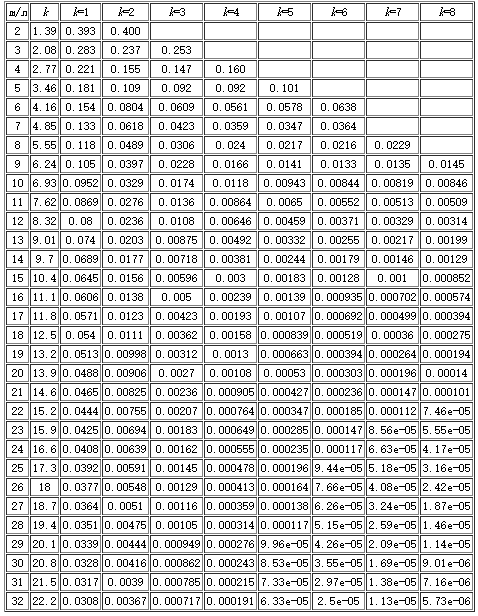
误判率的大小与 seeds 的数量、申请的内存大小、去重对象的数量有关，下面的表格展示了几个元素之间的关系：
- m 表示内存大小（多少个位），n 表示去重对象的数量，k 表示 seed 的个数；
- 假如代码中申请了 512M 内存，即1«32（m=2^32=4294967296，约43亿），seed 设置了7个。看 k=7 那一列，当漏失率为 8.56e-05 时，m/n 值为 23。所以 n = 43/23 = 1.86(亿），表示漏失概率为 8.56e-05 时，512M 内存可满足 1.86 亿条字符串的去重；
解决布隆过滤器误判方法
- TODO

在能容忍低错误率的应用场合下，Bloom Filter通过极少的错误换取了存储空间的极大节省；
对于爬虫工程师来说，布隆过滤器的典型应用是 高并发爬虫去重，正如文章开始时举的例子，如果爬虫的请求数量达到 亿计、十亿计 这个量级，那么布隆去重将是去重策略的首选；
除了爬虫之外，布隆过滤器广泛应用于数据库设计，例如：
- Google 著名的分布式数据库 Bigtable 使用了布隆过滤器来查找不存在的行或列，以减少磁盘查找的IO次数；
在很多 Key-Value 系统中也使用了布隆过滤器来加快查询过程，如 Hbase，Accumulo，Leveldb，一般而言 Value 保存在磁盘中，访问磁盘需要花费大量时间，然而使用布隆过滤器可以快速判断某个 Key 对应的 Value 是否存在，因此可以避免很多不必要的磁盘IO操作，只是引入布隆过滤器会带来一定的内存消耗；

注意：Bloom Filter 不适合那些 “零错误” 的应用场合；
缺点
- 有误判率，即存在假阳性(False Position)，即不能准确判断元素是否在集合中，接下来会细讲；
- 不能获取元素本身；
- 一般情况下不能从布隆过滤器中删除元素；
- 如果采用计数方式删除，可能会存在计数回绕问题；